How to Build a Query Engine

In our early days, all the queries doing sequence analytics and feeding the output to visualization layer were built using SQL underneath. Rather quickly, the code for generating these queries become complex and the queries themselves were massive and slow. The attempts to use MATCH_RECOGNIZE (a row pattern matching capability added in SQL:2016 and now available in multiple SQL query engines) were somewhat disappointing and we came to the conclusion that we must take a different path.

We didn’t yet have SOL back then yet. Just a small glimpse of a DSL (Domain Specific Language), prototyped by our CEO, Misha, in his Observable Notebooks. The critical part of the DSL (and the one we struggled the most while trying to express it via SQL) was a capability to match and reference sub-sequences of events in a flexible way. Essentially being able to use array semantics within a window of events for a specific actor. The fundamental issue with SQL is that it is not useful for expressing operations across rows (unlike across columns), which makes this a challenging task. Similar observation was made by Michael Stonebraker and Andy Pavlo in their excellent paper reviewing the landscape of database management systems, where they state that “(…) RDBMSs cannot efficiently store and analyze arrays despite new SQL/MDA enhancements.”.

When dealing with clickstreams or other types of sequence events, this sort of the capability matters a lot.  We looked at various available options as of 2022 and concluded that we really need a dedicated language to solve this problem, though borrowing multiple ideas from existing concepts, such as SASE+, Cypher syntax or regex capture groups.

To give an example, imagine having logs from a pet store and trying to:

1. Find cases when the same product is being looked at twice before adding to cart.
2. When it occurs, measure the duration since seeing the product for the first time to adding it to cart.

This category of problem is surprisingly hard to express using SQL, yet it can be written in a remarkably elegant way when using SOL (Sequence Operations Language), which uses much more fitting abstractions for sequence analytics.

We spent a good amount of time on SOL and iterating over it. In our initial plans it was supposed to be just an internal layer, used by visual editor components and allowing us to move fast. However, it turned out to be so powerful that we felt the urge to share it with the world, made it a central point of the experience working with Motif and announced it publicly in 2023.

The overall architecture

Getting the results from the queried dataset involves several steps. As the user enters a SOL query, it is then processed and executed top-down as in the following diagram.

Parsing

The first step is to actually parse the provided string. We use Ohm, which provides a nice layer for working with PEG (Parsing Expression Grammar) and yields an AST (Abstract Syntax Tree) model on the output.

Post-processing and error handling

Error handling and all of the things which cannot be handled by the grammar itself are handled immediately after. This allows to resolve some ambiguities (e.g. determine types of the references) and make the errors more human readable. Just to give an example, it is much easier to reason about this:

Than trying to figure out what to do after seeing invalid token at position 6 or so.

Abstract Syntax Tree

After successful parsing, it outputs the AST representation of the query, which allows to build the automata and evaluate expressions. For a sake of the example, lets look at the output for following query:

match A(product_page)

The query matches a single event named “product_page” and puts it under tag “A”.

Tags allow to mark and access (reference) matched events and their dimension values. You can consider tags a variation of named capture groups in regular expressions.

The output is somewhat verbose so lets just look into the relevant AST sections. The first one is the actual pattern match model. It describes a single tag, aliased (named) “A”. It also says it expects to match exactly one occurrence of it.

"pattern": {
  "tags": [
    {
      "alias": "A",
      "quantifier": {
        "min": 1,
        "max": 1
      }
    }
  ]
}

Following the match pattern, the next section contains the conditions (predicates) which must be met each of the match tags. In our case, this is just one predicate:

"if": {
  "predicates": [
    {
      "alias": "A"
      "type": "RELATIONAL",
      "operator": "=",
      "arg1": {
        "alias": "A",
        "dimensionName": "name",
        "type": "EVENT_DIM_REFERENCE"
      },
      "arg2": {
        "arg1": "product_page",
        "arg1Type": "string",
        "type": "LITERAL"
      },
    }
  ]
}

Decoding it should be rather straightforward. It’s a relational equality expression, meaning there are two arguments which must be equal to each other. One is name dimension of tag aliased with “A”. The other is string literal “product_page”. This builds a condition which will be true when the name will be equal to “product_page”.

Building the automata

Having the AST representation of the query, we can now start building the automaton (one for each MATCH statement). It’s a process which itself consists out of several steps (as a refresher, we highly recommend “Automata Theory: inside a RegExp machine” course at Udemy). In our case, this is:

1. Building the NFA (nondetermininistic finite automaton).
2. Converting it into a pseudo-DFA (deterministic finite automaton) table. Due to expressivity of SOL, we’re not strictly able to convert NFA into a fully deterministic automata, yet we still convert it into a state-transition table, which reduces the overall number of transitions to check.
3. On top of that, we create a sequence of operations executed after running the match automaton (e.g. REPLACE or COMBINE statements).

It is not strictly necessary to build DFA and some regex libraries are actually using NFA instead. This allows to save memory and keep implementation simple, as in many cases DFA’s end up having much larger number of states than the NFA’s. Also, in our case, the transition functions can be quite complex, reference previous matches (tags) in their arguments and require backtracking to traverse the search tree until finding a solution (if one exists).To deal with it, we have a somewhat hybrid approach (which we call “pseudo-DFA”), where we follow the steps of creating a state-transition table from NFA graph (including exploring epsilon-closures), but still allow for multiple transitions from a given state, just order them by priority and support backtracking.

Basic example

Taking our example AST from above (slightly oversimplified, will explain in a minute), lets examine what would be the output. In the very basic form, we would get following transitions (both the NFA graph and pseudo-DFA transition table are presented):

The graph has three circles, each describing a specific state. For a single-event match, we have three of them:

• before:A, which is associated with entry point for testing if it is an A match; it has only one transition, labeled as A, which tests if all the predicates associated with A are all true before going to the next state and consuming the event; in our case, it will check if name is equal to “product_page”
• event_match:A, which marks a successful test result; it has only one, ε (epsilon) transition, which allows to switch to next state spontaneously (without consuming any event,
• after:A, the accepting (final) state (hence the double border), which marks end of a match and allows to exit

Converting this graph to a pseudo-DFA table reduces the number of states to two (indicated in the first column):

• 0, from which the only allowed path is to 1, through predicates associated with A
• 1, which is the final, accepting state and does not allow any further transition

PREFIX and SUFFIX

The automaton above would easily match a single-event sequence containing an event named “product_page”. But what if it contains other events?

As mentioned previously, the example was slightly oversimplified. In fact, it can match only a single-event sequence. In real life, we usually want is to allow for any other preceding and succeeding events, as needed, so the whole sequence containing the searched event is matched.

We call these PREFIX and SUFFIX respectively. We imply these are always present, unless using special anchors. The example from above would expressed in SOL as  MATCH START >> A(product_page) >> END.

When the anchors are skipped (default behavior), the automaton gets more complex, though one can start seeing building blocks there.

Lets focus on the transition table. As we start with the beginning of the sequence, there are two possible transitions:

• one labeled as A (when name="product_page" and with priority=1), moving to state 1
• another labeled as PREFIX (on any input), with lower priority=4 and keeping the state at 0

We evaluate the transitions according to their priority, so we first check the condition name="product_page". If it’s true, we move to state 1 and mark the event as A. Otherwise, we try the other transition, which marks the event as PREFIX and stays at state 0.

When automata eventually moves to state 1, it can either accept the sequence (if there are no further events) or immediately follows to state 2, where it accepts any further events and keeps marking them as SUFFIX until the end of the sequence is reached. A sample matched sequence might look like following:

Quantifiers

Of course, matching exactly one event is somewhat limitting. SOL supports all sorts of quantifiers, which you might know already from regular expressions:

• ? (zero or one match)
• * (any number of matches, as in Kleene closure)
• + (one or more matches)
• {m,n} (any number of matches between m and n)

Adding a quantifier impacts the automaton by adding extra epsilon transitions or increasing the number of states (for {m,n} quantifiers). For example, match A(product_page)* yields following output:

Now, when the automata is in state 1 and the current event matches the associated predicate, it will keep appending it to tag A as long as possible. For example, it can match following:

Tags are the building blocks

As more tags are added to the query, the automaton becomes more complex and both the graph and state transition representations take more space. This makes it challenging to read, though one way to reason about it is that each tag (with its specific set of transitions) is a single building block of the automaton graph, appended serially per its position in the match statement.

Lets take the query solving the problem brought in the intro for consideration:

match 
  A(product_page) >> * >> B(product_page) >> * >> add_to_cart
if 
  A.pid = add_to_cart.pid
and 
  B.pid = add_to_cart.pid
set 
  time_since_first = duration(A, add_to_cart)

As the corresponding automaton graph got much larger, the layout is adjusted a bit. You can notice the building blocks for each of the matches in it.

To see how it works, consider a simple, 4-event sequence and steps required to match it fully. This sequence does not require backtracking. To make it less verbose, we’ll be following the state transition table. The transitions are sorted according to priority. In each state we test the available transitions until one is true and keep following the transitions until all events are consumed and automata is in accepting state.

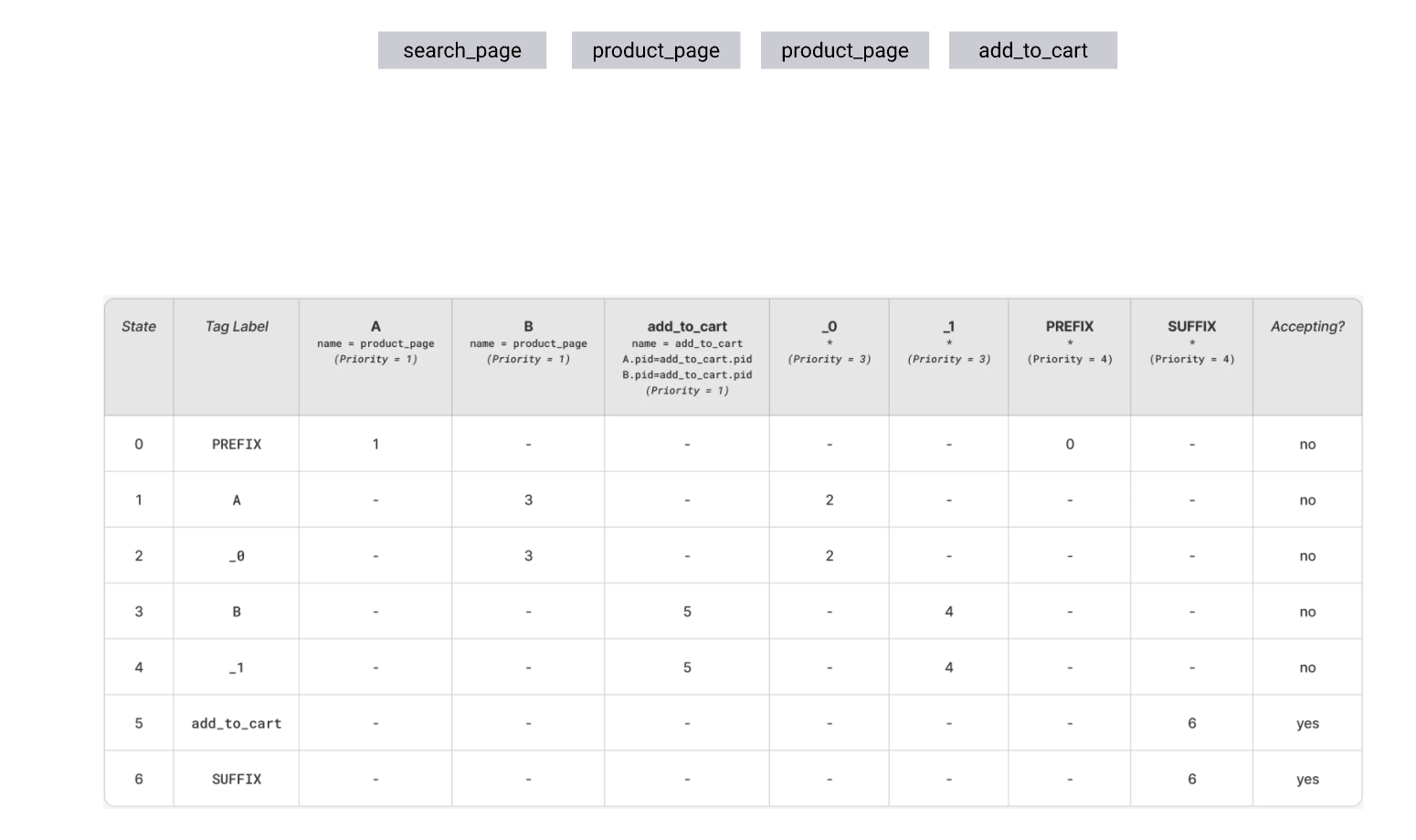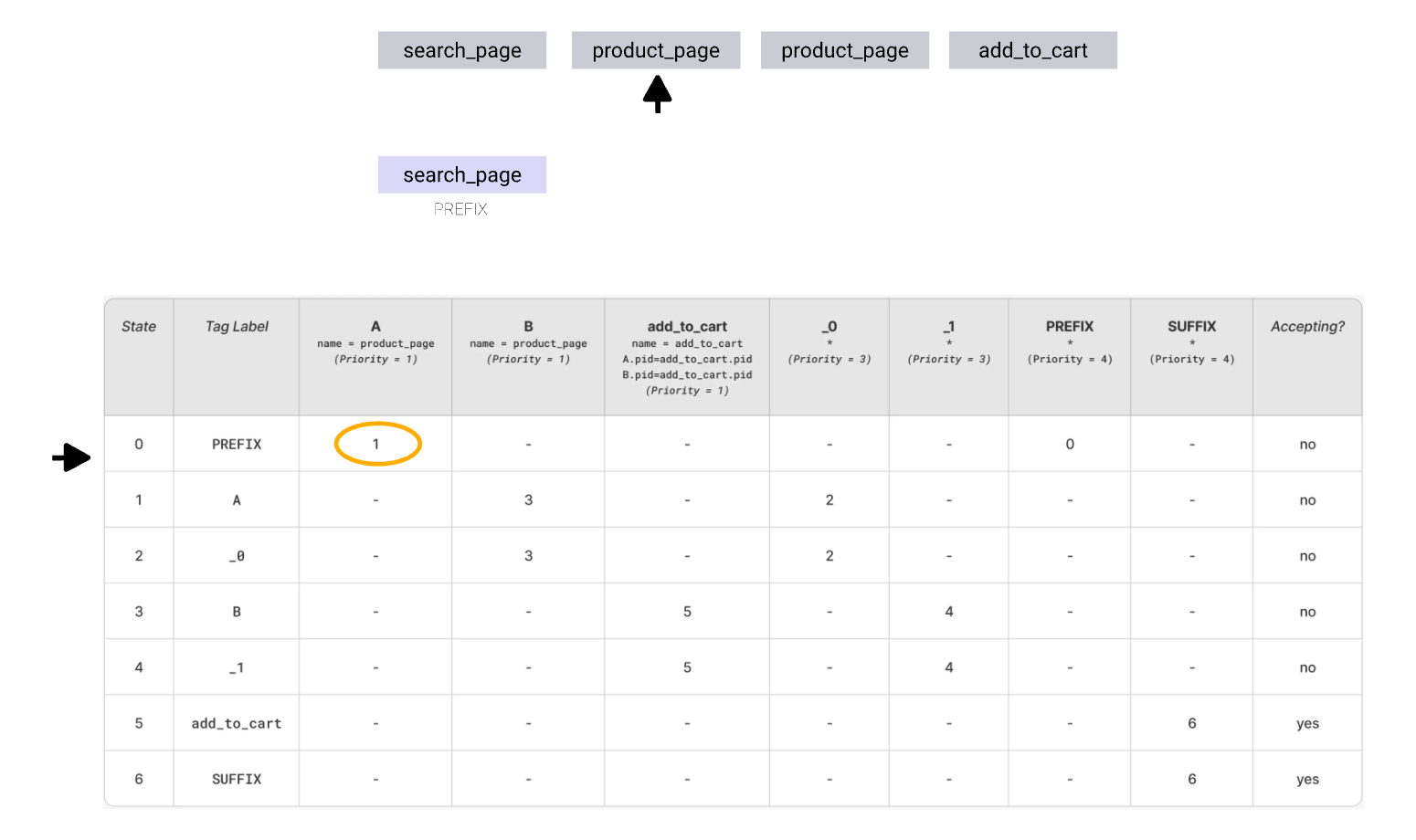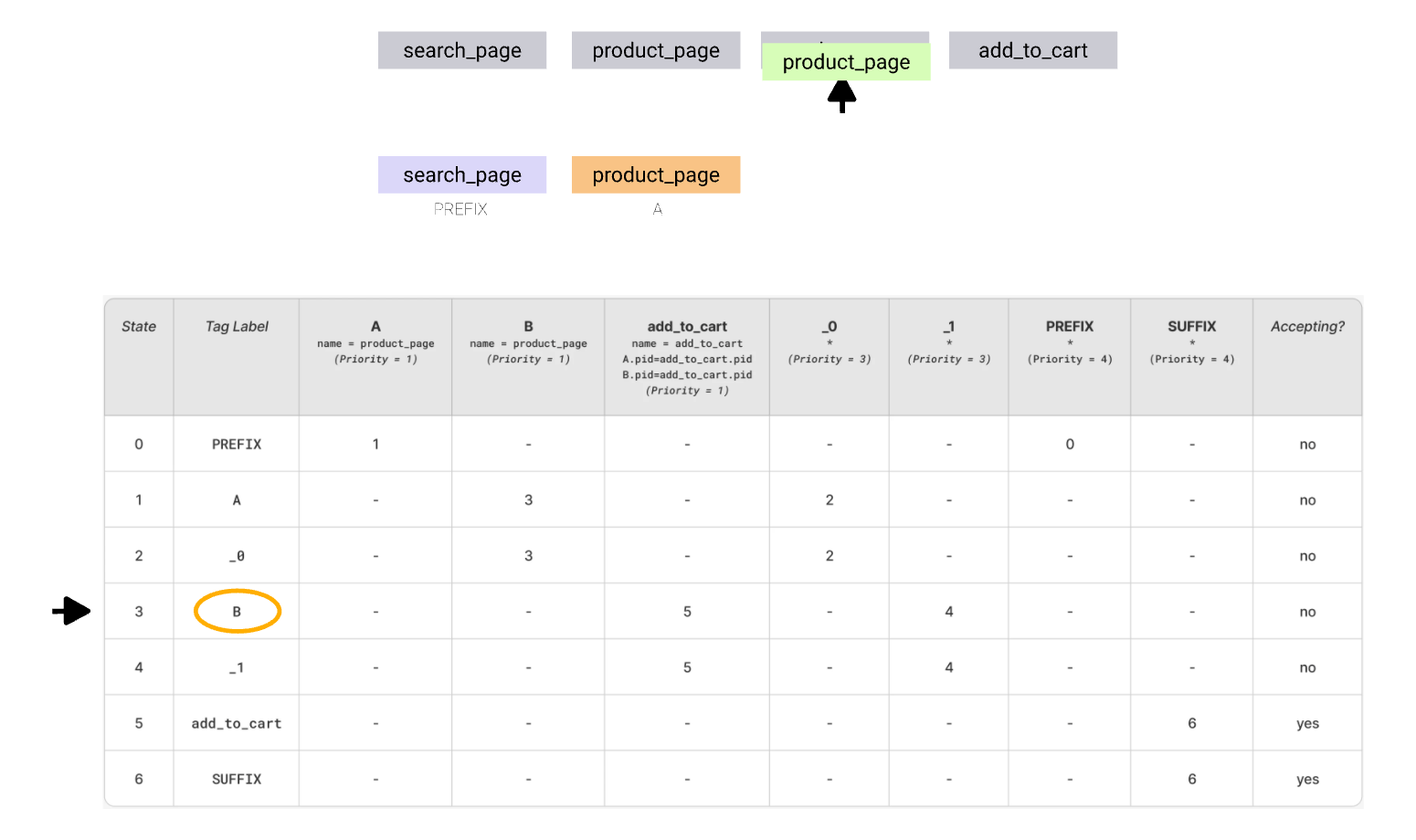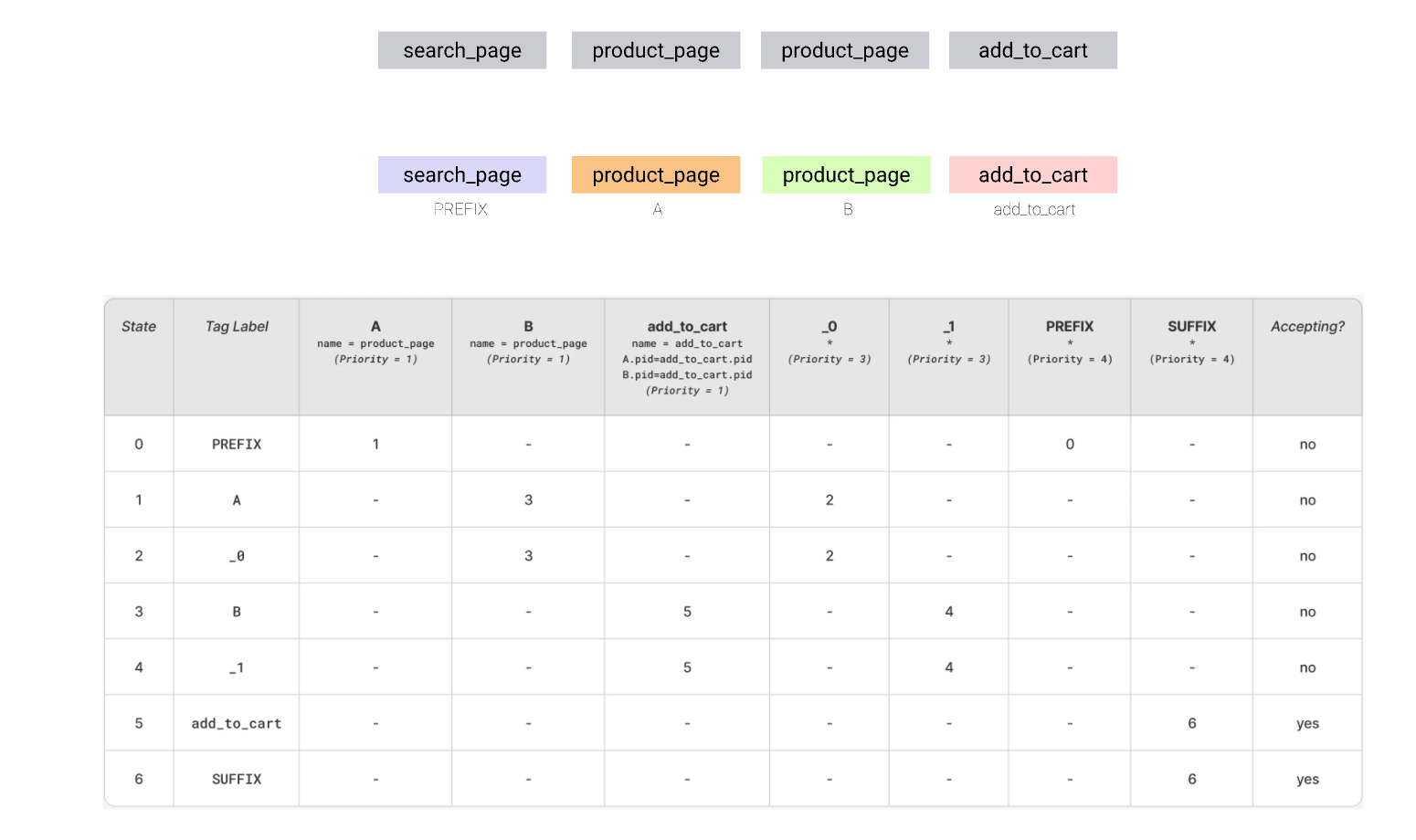
Backtracking

The above example is somewhat optimistic though and it shows how the automata proceeds when no backtracking is required. It might have been mistaken for a continuous list of the steps, though in reality, match statements are declarative rather than imperative. I.e. they describe what conditions must be met for match to happen rather than what steps are required to execute them.

Finding the solution can be solved with backtracking, which is a bit like navigating a maze. When you reach a dead end, you need to go back to the previous intersection and continue from there using a different route.

The following sequence is bit harder than the one in the previous example. Following the optimistic path will eventually lead to add_to_cart transition failing due to “pid” condition not matching:

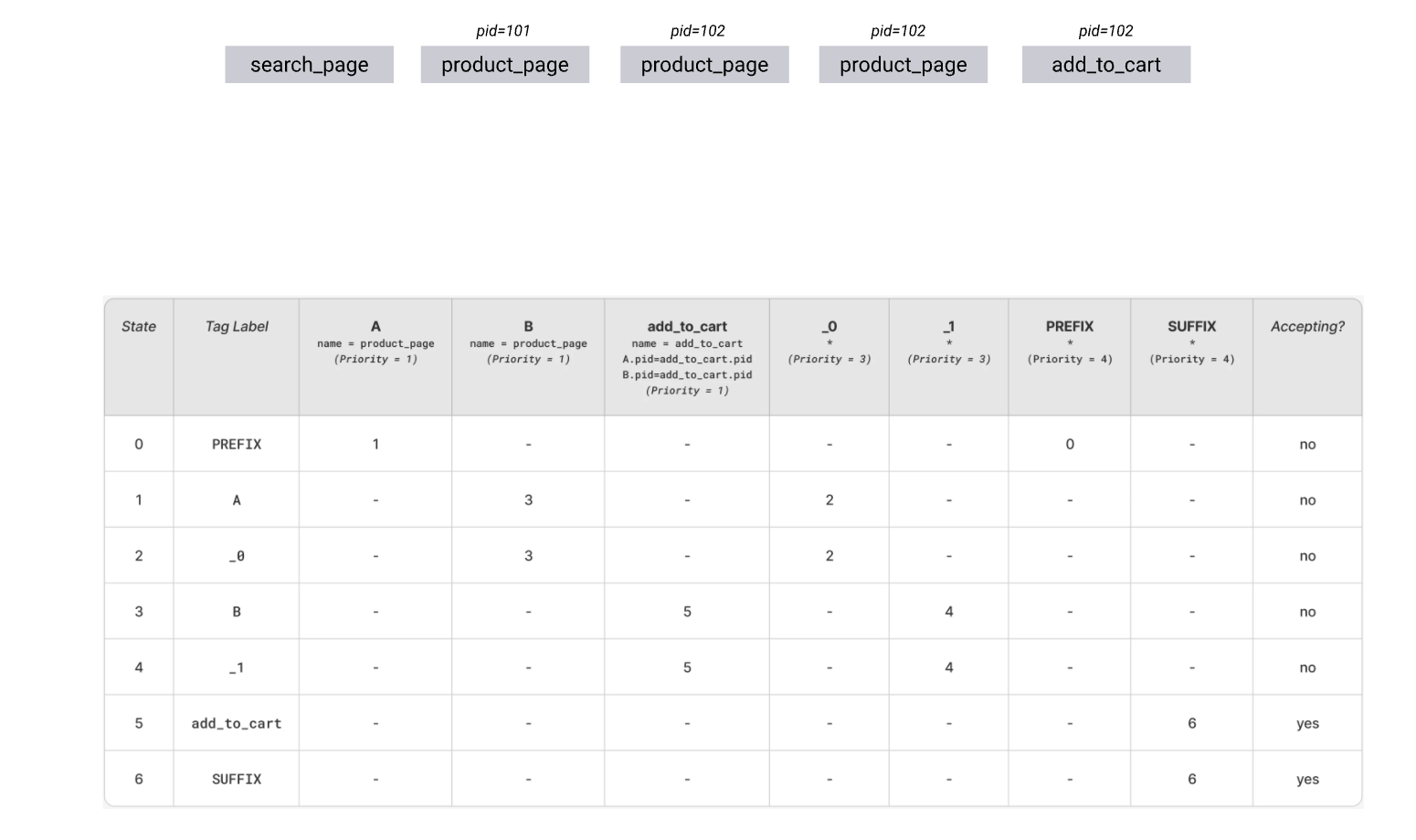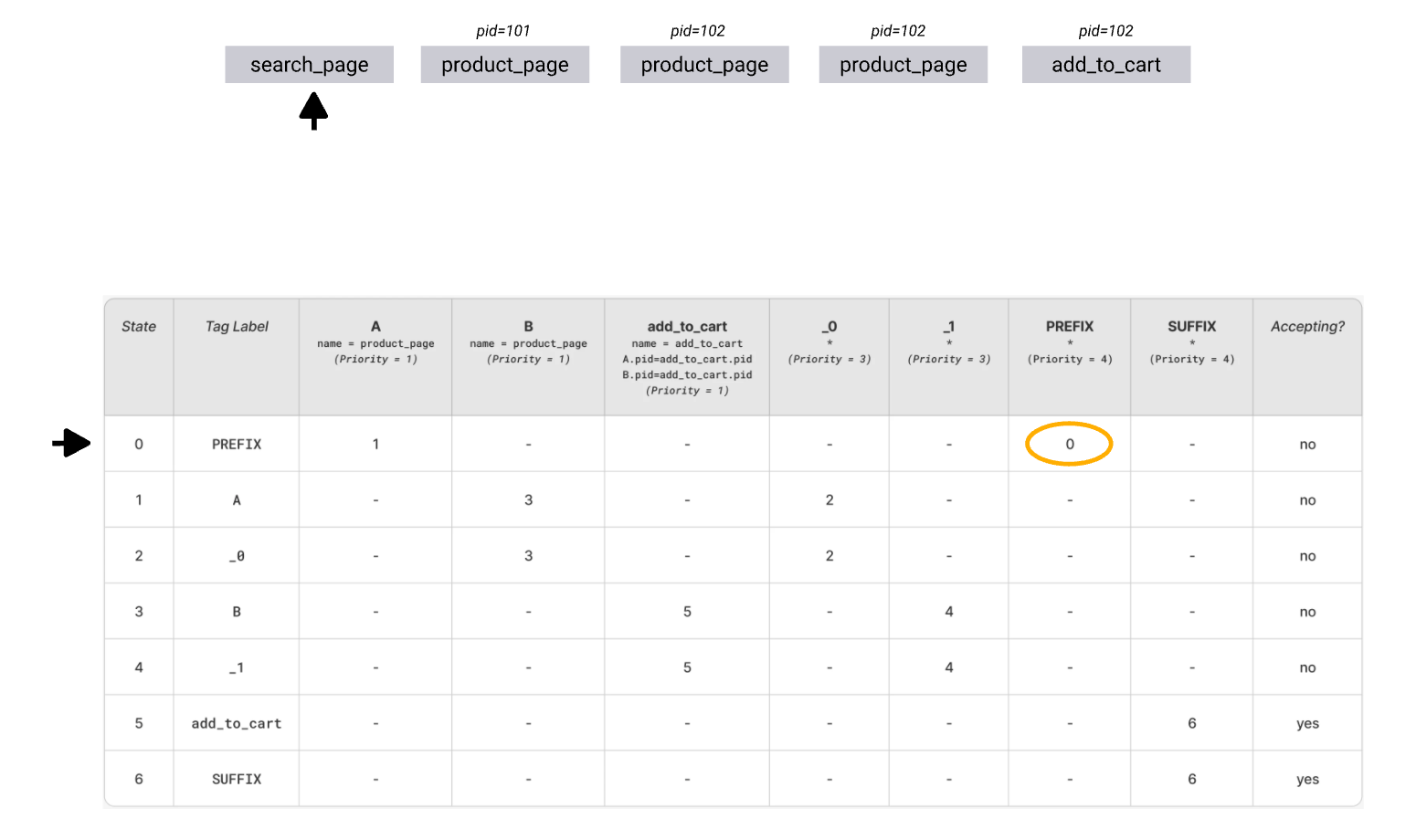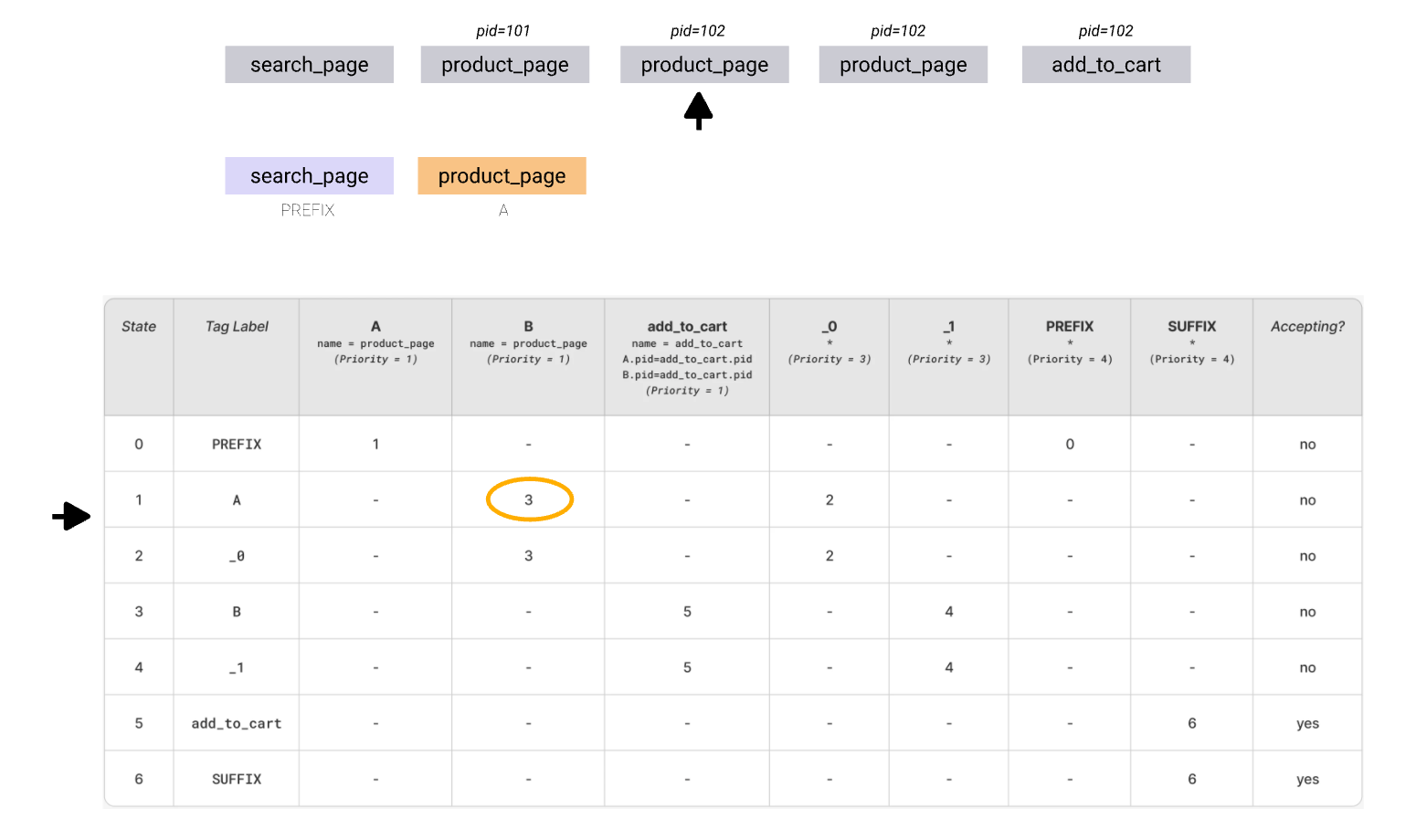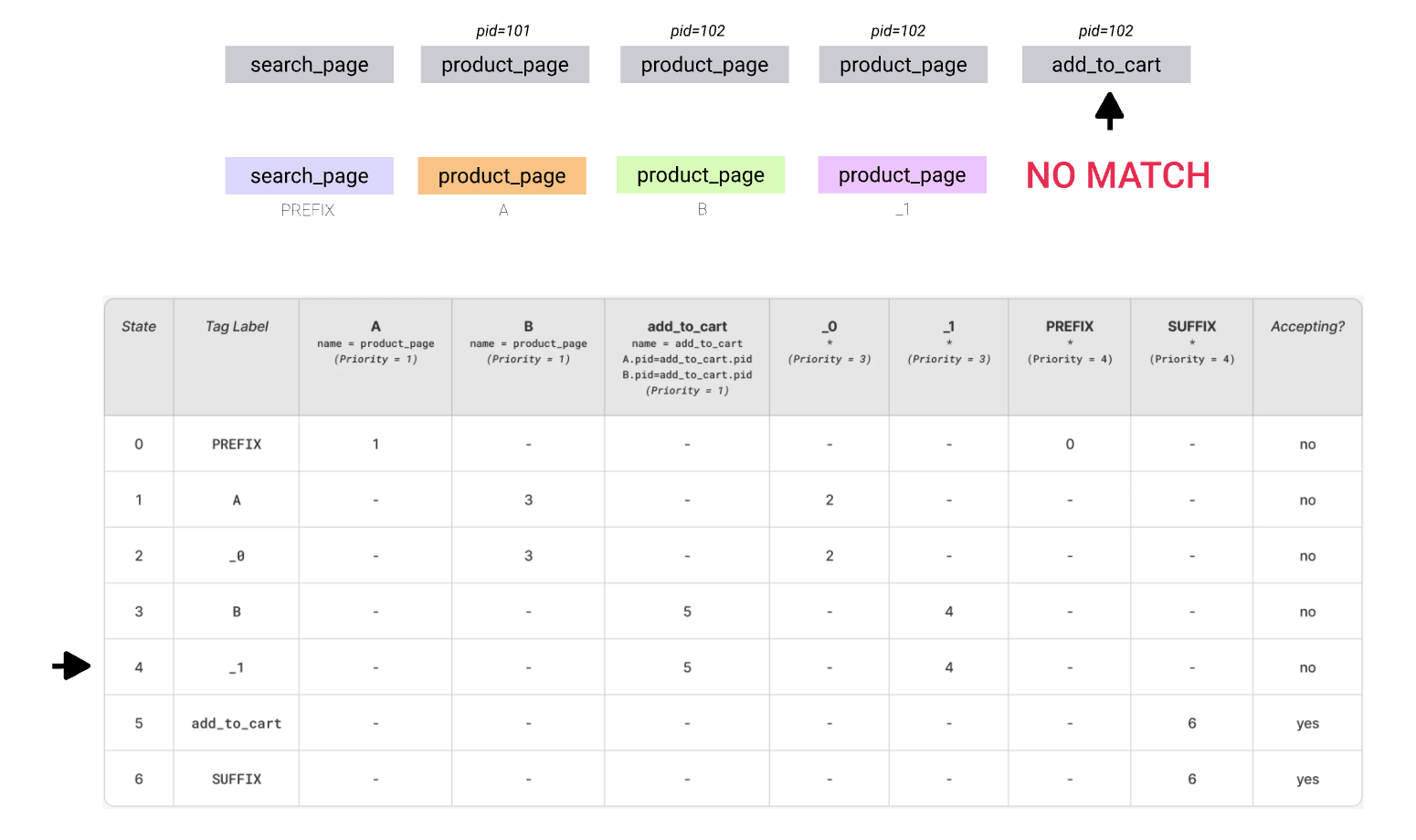
The automaton needs to backtrack and keep trying the other available transitions until it succeeds or all transitions are exhausted. The continuation of the search can be observed below (in a somewhat simplified form)

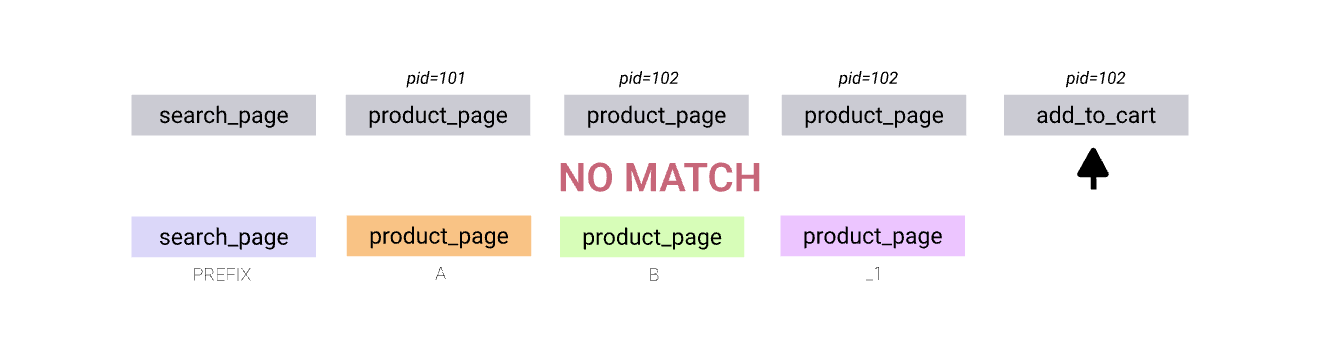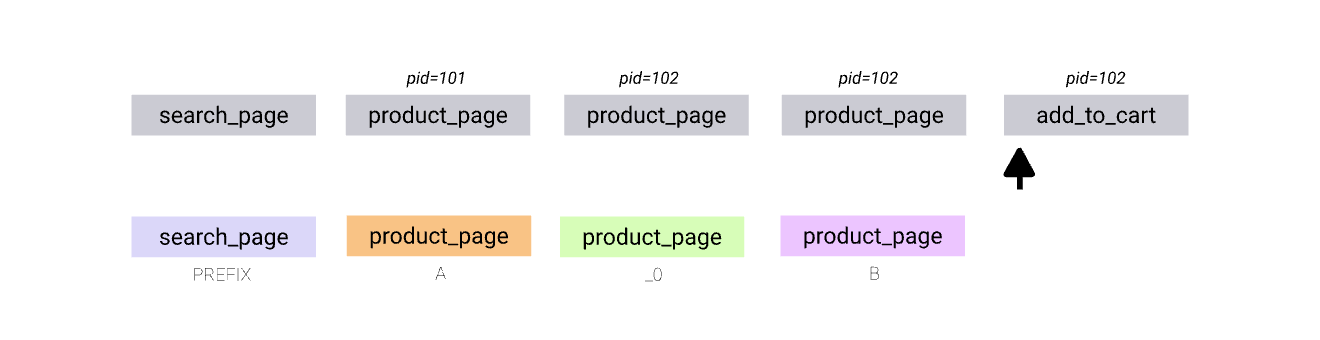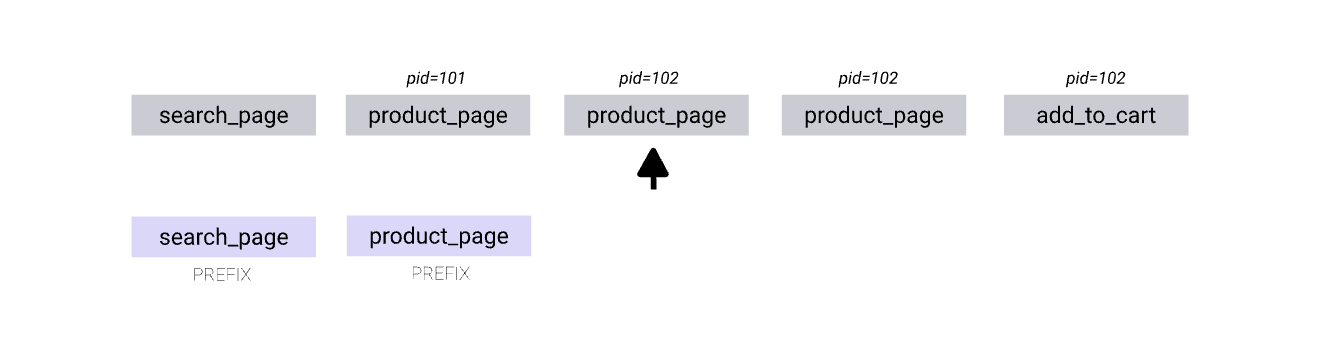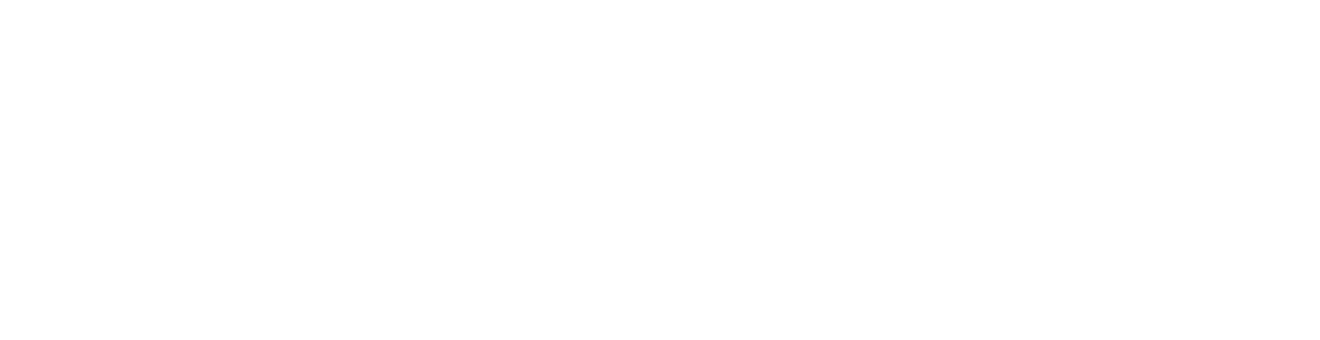
Search space

As we noted, the match pattern is in fact a declarative statement, which means that it describes what kind of pattern we are trying to find in the sequence (if present) rather than how to build it. Depending on the actual pattern and predicates, the search space can be quite vast. The role of the automaton is to traverse it in a prioritized way, until end of the sequence is reached and the final state is an accepting one or all possible transitions were exhausted and the query does not match the sequence.

This can be visualized using a tree describing all possible transitions for the sequence and query from the previous example. The actual tests made by automata are marked at each transition.

As you can imagine, when the match patterns gets more complex, the actual search space becomes even bigger. Some of the queries are quite expensive to run, though many of the non-matching cases can be pruned out. For example, if there’s a simple condition that needs to be matched for at least one event (e.g. “A.foo=1234”) and it’s never true for a particular sequence, the automaton does not even need to be executed on it.

Initially-False/Initially-True Predicates

By building the SOL as a declarative language, we also aimed at making it intuitive to use with tags consisting of any number of events. This had interesting side effects for some categories of queries.

Consider the following predicate example. Essentially, trying to use an aggregation function on a multi-event tag dimensions. In this case, calculating duration between the first and the last event in a matched tag (where user was viewing product_pages continuously for more than 5 minutes).

match 
  product_page+ 
if 
  duration(product_page[0],product_page[-1]) > 5min

Note: product_page[0] references the first event of the matched tag. product_page[-1] references the last event of the matched tag. duration(...) implies it’s used on the ts field, which describes event timestamp.

Now, let’s imagine the consecutive product_page events had following timestamps:

• 09:00am
• 09:01am
• 09:06am

The problem is evident already at the first event. As the automaton is iterating and starts with the first product_page, the tag has just a single event. Duration between 09:00am and 09:00am is zero, so it does not match the duration(…) > 5min condition…

Even if we would create some sort of exception and only start looking at the second event, it would be still not enough. Only after having the first three events, the predicate finally evaluates as true.

To capture this category of matches, we extend the automaton to cover two types of cases:

• when the predicate is initially true, continue until it becomes false (like we did beforehand)
• when the predicate is initially false (like in our example), keep trying until it becomes true, then keep running as long as it’s still true

We use this feature only in case of +1 predicates (such as * or +). It expands the search space even more, though it allows for some exceptional flexibility of the language and finding complex patterns, even some crazy ones, such as match A()+ >> B()+ if sum(A.foo) = sum(B.bar)

Post-automaton Expressions

Building and executing the automaton is usually the most complex and processing-intensive part of the whole process. After all matches are set and tags are associated with events, the engine executes the remaining operations, which access the specific events directly or via the (now available) tags.

For example, SET statement can reference the tags and assign or calculate some formulas:

Similarly, REPLACE can be used to transform or remove events from sequences using the tag names as references:

The post-automaton operations can be also executed on the whole sequences. To keep only sequences matching some specific criteria, FILTER statement needs to be used

Mutating Arrow Data

We use Apache Arrow as the underlying data model, which is the de-facto standard of in-memory columnar storage today. This makes it easier to integrate external libraries for input/output or integrate our engine with third party tools. While Apache Arrow is great for interoperability and reading/writing data, it is not optimized for mutating data. And this is a problem, since many of the operations we support, such as SET or REPLACE are built in a way which does mutate data. To deal with it, we use two techniques.

The first one is having an in-memory event view which describes which of the Arrow Vector (column) indexes represent each event in a sequence. For example, for the first sequence in the dataset which has 5 events, this can be [0,1,2,3,4]. If the second sequence has 3 events, it will be represented by [5,6,7] and so forth. Now, if the second event of the first sequence is to be removed, the array will now contain [0,2,3,4]. Using this technique the events can be reordered or even added to the sequence. E.g. if the whole dataset contains 10,000 events and a two new ones ares added to the first sequence, it might now contain indexes [0,2,3,4,10000,10001].

The second technique is having a vector overlay over the immutable Apache Arrow Vector. It might be also considered a type of a write-through cache. When the value is mutated, we simply use an additional sparse JavaScript array and set a new value under the given index. When reading, we first check for the value in the overlay layer and if it is not set, read from the original Apache Arrow Vector. This arrays can be also easily grown if a new event is added.

A more complex example presents the diagram below. We use a mix of removing the events, updating the values and replacing one event with two other ones.

The output of this overlaid vectors can be converted back into Apache Arrow, if needed, though more frequently it’s a subject of Motif-specific aggregations (such as our Metrics API).

Performance and Stability

If you read through all of this and you are concerned about overall performance of this (or just curious if we have any troubles with stability) then let me say this are great questions. Even if our engine is currently implemented using TypeScript, it’s reasonably fast. So fast, that our SOL code execution times are typically on par with times to read a Parquet file into Apache Arrow in memory model. The fastest technique we found for the latter is using DuckDB NodeJS library, which means that it runs using native library code (implemented in C++).

It’s possible to write SOL queries which have quadratic computational complexity (depending on the number of events per sequence), though most of them are linear in nature and we observe per-CPU throughput in the order of 500k-2M events per second. To get there, we spent quite a bit of time optimizing the code and improved our original numbers by an order of magnitude since the initial implementation. There are several techniques which help with this (e.g. replacing conditional blocks with closures, push-down predicates on actor ids, filtering the fetched dimensions or pruning sequences) which are perhaps worth another blog post.

As for the stability and accuracy, we were prioritizing this since day one and other than taking extra care during development and reviews, we implemented a massive suite of test cases. It consists of (literally) several thousands of test cases like this one:

expect('MATCH SPLIT A(a)').toYieldBufferedSequence(
  'babab',
  'PREFIX(b)|A(a)SUFFIX(b)|A(a)SUFFIX(b)'
);

Needless to say, bugs do happen in every computer system though these seem to be rare with our query execution engine. During the last 12 months we saw around 100,000 queries executed overall and we are aware of just one case of a SOL-specific bug discovered during that time.

Summary

As an array database, SOL offers capabilities that are not readily available or easily implementable in SQL. The ability to express complex patterns, handle time-based sequences, and perform advanced matching operations gives it a distinct advantage in scenarios where event order and relationships are crucial.  Our users love it and can now perform analyses that were previously out of reach or required extensive (and complex) workarounds.

To make it easier to adopt for current SQL lovers, we're investigating how we can extend SQL with some of the powerful features we've developed for SOL, potentially offering a hybrid solution that combines the familiarity of SQL with the advanced sequence analytics we built at Motif. This ongoing exploration reflects our commitment to continual improvement and our recognition that different users and use cases may benefit from varied approaches.

We're curious to hear your thoughts on this. Have you encountered situations where traditional SQL fell short for sequence or event-based analytics? Do you see value in a specialized language like SOL, or would you prefer extensions to SQL? Your insights and experiences could help shape the future direction of our query engine development. Feel free to share your perspectives, either in the comments on social media or at hello@motifanalytics.com

‍